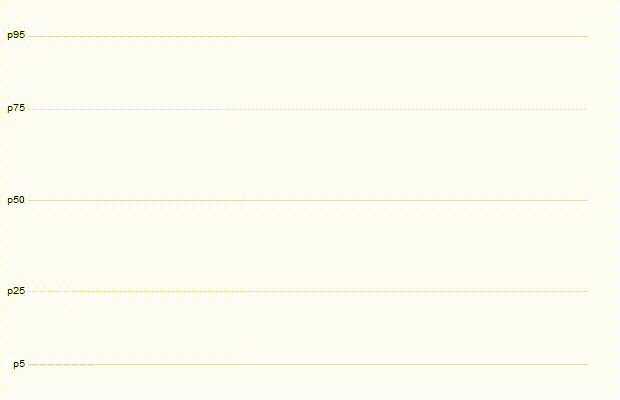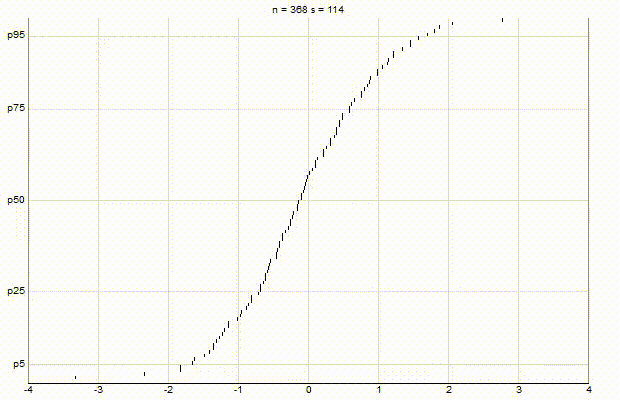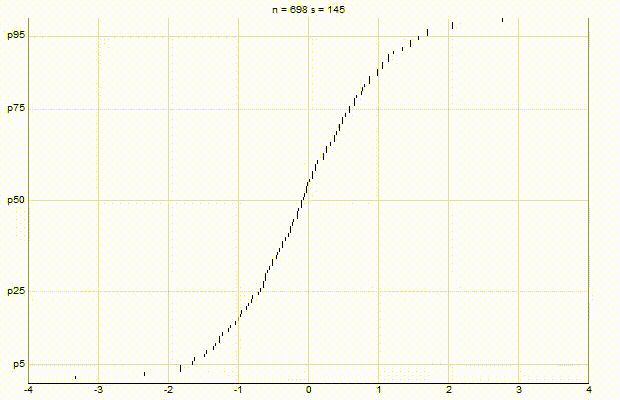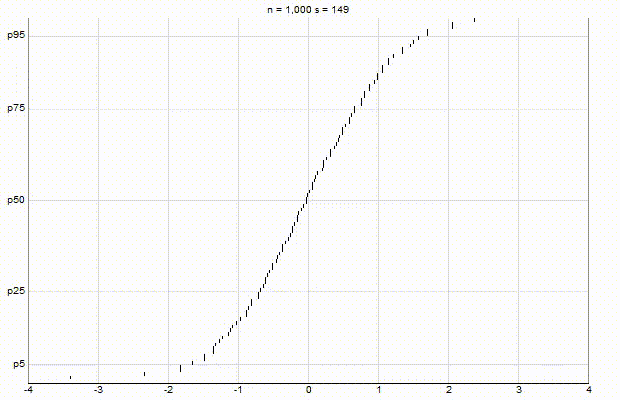
This is part 3/8 of my Calculating Percentiles on Streaming Data series.

In an effort to better understand the Greenwald-Khanna [GK01] algorithm, I created a series of visualizations of the cumulative distribution functions of a randomly-generated, normally-distributed data set with $\mu$ = 0 and $\sigma$ = 1, as the number of random numbers $n$ increases from 1 to 1,000.

The way to read these visualizations is to find the percentile you are looking for on the y-axis, then trace horizontally to find the vertical line on the chart which intersects this location, then read the value from the x-axis.

Exact:

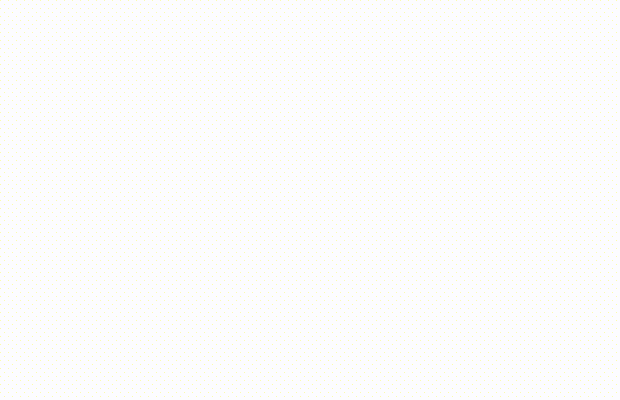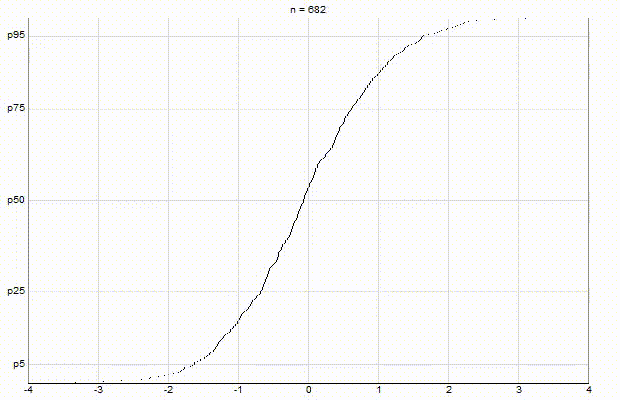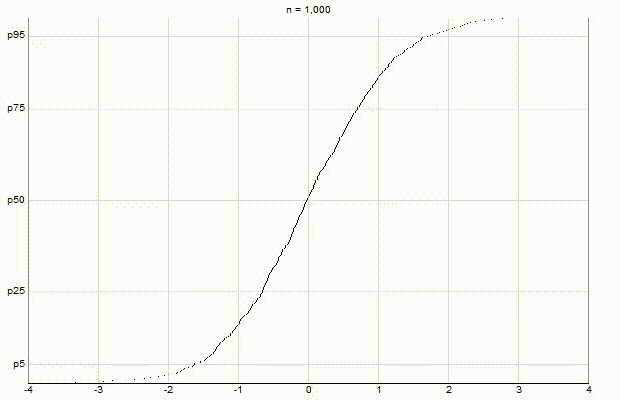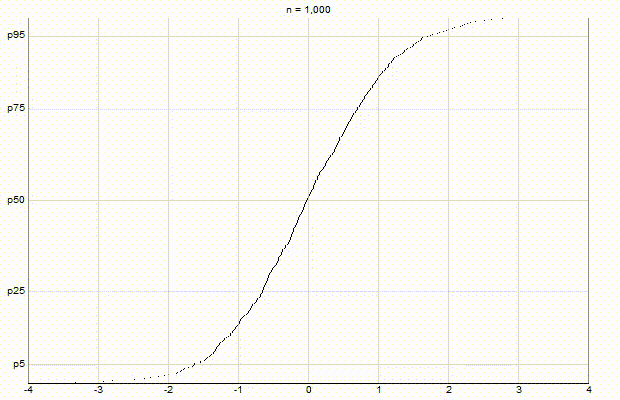
Greenwald-Khanna $\epsilon$ = 0.1:

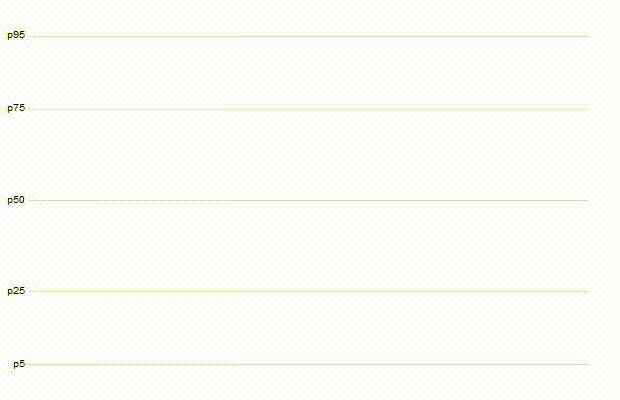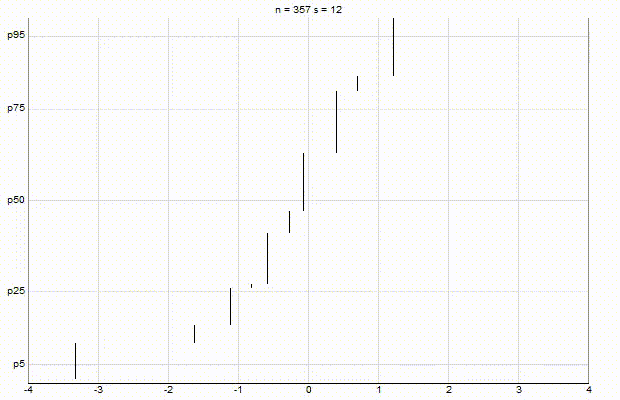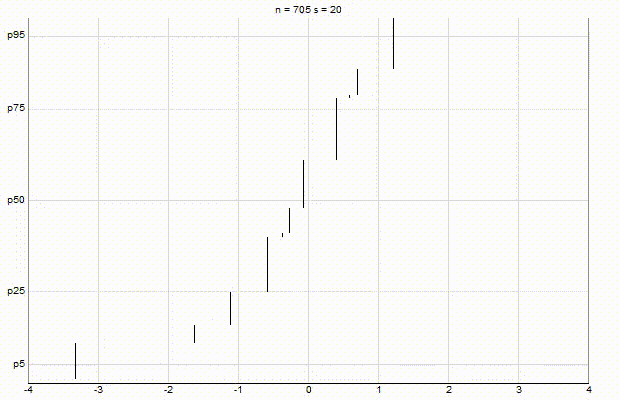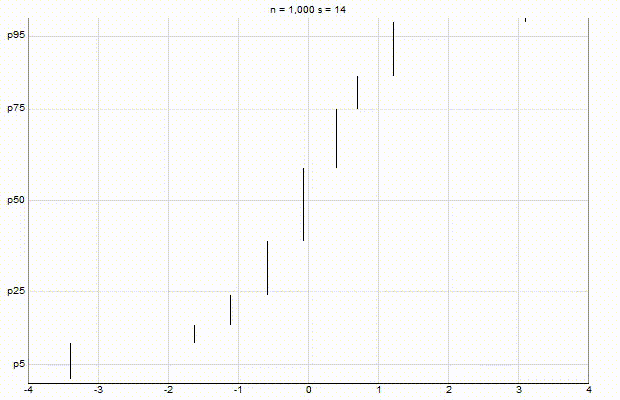
Greenwald-Khanna $\epsilon$ = 0.05:

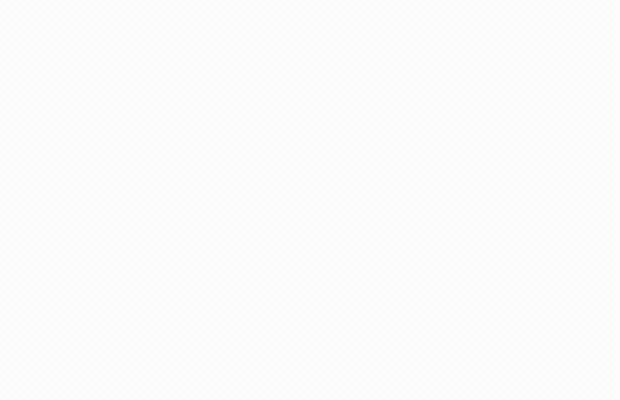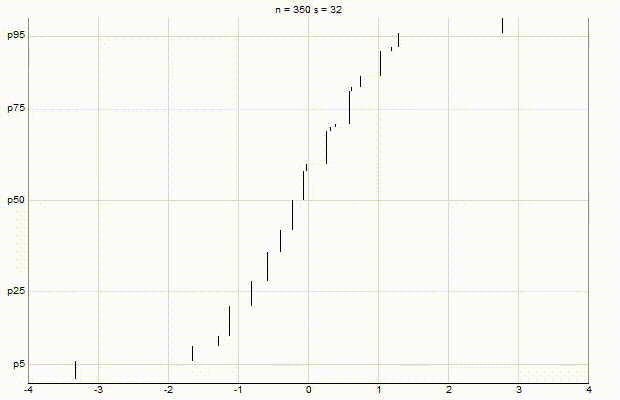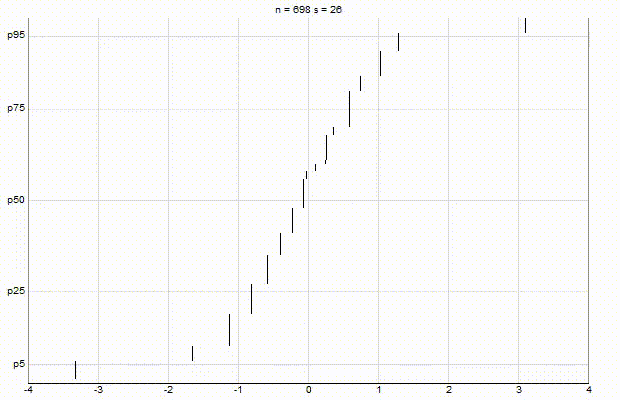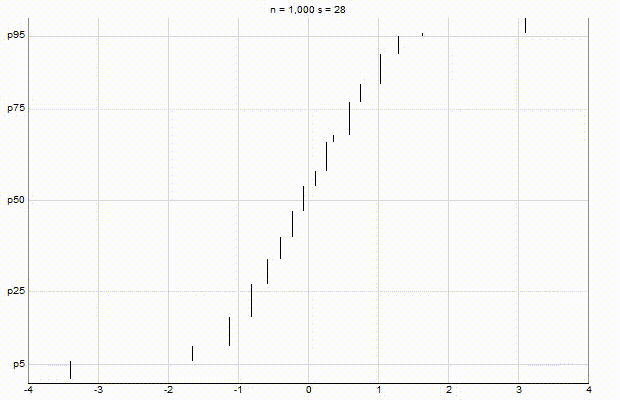
Greenwald-Khanna $\epsilon$ = 0.01:

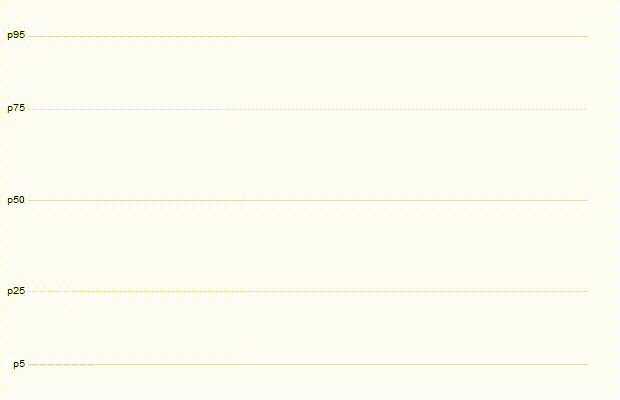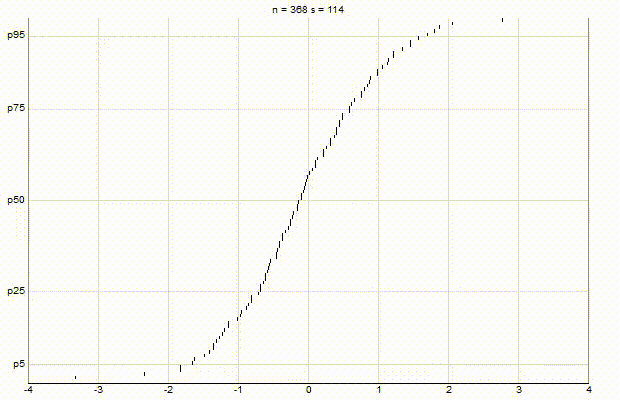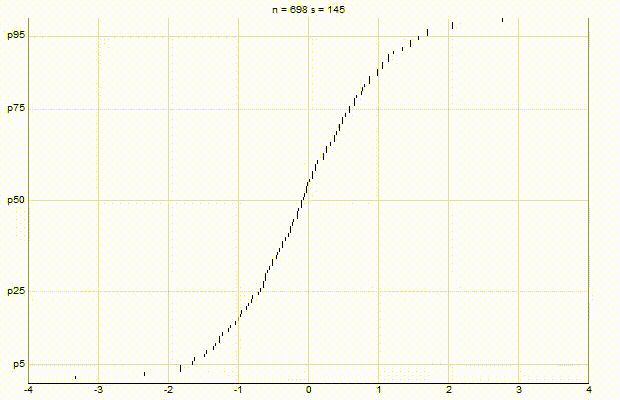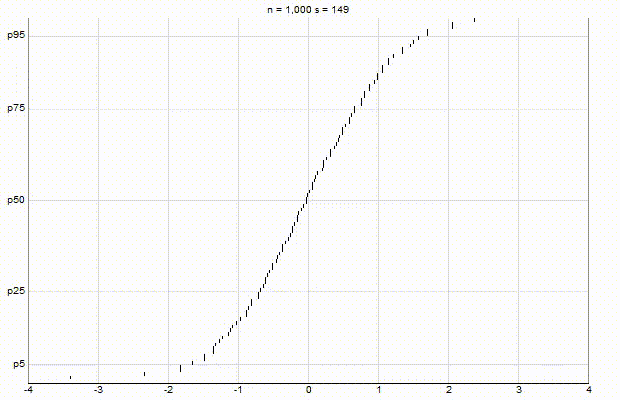
From these visualizations, it is quite intuitive and clear how the “resolution” of Greenwald-Khanna increases as $\epsilon$ decreases, and how the compress operation keeps the number of elements in the summary data set $\mathsf{S}$ relatively small as $n$ increases.

References

• [GK01] M. Greenwald and S. Khanna. Space-efficient online computation of quantile summaries. In Proceedings of ACM SIGMOD, pages 58–66, 2001.