
This post describes how to implement the OpenSSF Compiler Options Hardening Guide for C and C++ in CMake.
Read more...
My name is Steve. I am a Principal Engineer at Relativity and an Adjunct Professor of Software Engineering at DePaul University.
I have blogged on-and-off since 2004. Over the last 20+ years, I have published a number of blog posts, blog post series, links, and projects on this website. I also have a number of open source projects on GitHub.
For more about me, see my about me page.

This post describes how to implement the OpenSSF Compiler Options Hardening Guide for C and C++ in CMake.
Read more...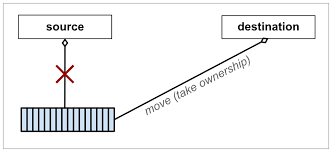
After trying out the Movable<TResource> type from Move Semantics for IDisposable
I discovered a fatal flaw in its implementation: it is incompatible with struct
memberwise copy semantics.

See also Move Semantics for IDisposable Part 2
C++ 11 introduced the concept of move semantics to model transfer of ownership.
Rust includes transfer of ownership as a key component of its type system.
C# could benefit from something similar for IDisposable types. This blog
post explores some options on how to handle this.

Downloading a private release asset from GitHub given only its name and tag requires a complicated series of interactions with the GitHub API. This blog post explains how to write two repository rules which make dealing with private release assets in Bazel easy.
Read more...
A quick tip on how to execute multiple run commands in parallel.
Read more...